The Koch Snowflake
This project draws a fractal curve, with only a few lines of turtle graphics code. It assumes you know about for-loops and functions. And it introduces the computer science idea of recursion.
The basic unit
Start the project by making an empty file koch.py.
Right-click and open it with IDLE.
We’re going to define a function that either
draws a line with a kink in it,
or draws a straight line the same length.
Which one it does
will depend on whether the argument order is greater than zero.
Type this in the editor, save it (ctrl-S) and run it (F5):
# Draw a Koch snowflake
from turtle import *
def koch(a, order):
if order > 0:
for t in [60, -120, 60, 0]:
forward(a/3)
left(t)
else:
forward(a)
# Test
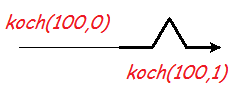
koch(100, 0)
pensize(3)
koch(100, 1)
The symbol > means “greater than”.
Be careful about the indenting (the spaces before each line).
You should get this:
Recursion
This is where your head explodes.
You will replace the forward(a/3) with another call to koch,
to draw a kinked line of the same length.
That’s a line with 4 parts, …
and each of those parts has 4 parts,
and each of those parts has 4 parts,
and each of those parts has 4 parts, …
Well, not in practice.
In practice,
the variable order goes down by one each time,
and when it hits zero, we just draw a line.
Change the function koch, just a little:
for t in [60, -120, 60, 0]:
koch(a/3, order-1)
left(t)
When a function calls itself, we say it is recursive. Recursion can solve problems that simple iteration (like a for-loop) cannot.
Save and run. You will get the same two curves as before, because of the test code. But try this in the shell:
>>> reset()
>>> koch(100, 2)
Now each line segment has become a Koch curve. There are 16 little lines.
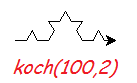
What happens for koch(100,3) or koch(100,4)?
The order 4 curve has 256 tiny lines.
One thing that happens is that it starts to take a long time to draw.
A call to speed("fastest") before you start drawing will help.
Need for speed
The drawing is still too slow once order is 6 or more.
(The calculation is fast.)
The turtle module wants to show you every change as it is happening:
good when debugging,
not so good when you just want the result.
We can delay putting the actions on the screen with the tracer function.
But then we have to tell it to appear using the update function,
when we’re ready.
Looks like snow
The snowflake is made from 3 Koch curves. Although there are only 3 “sides”, it has 6-fold symmetry, like a real snowflake.
Delete the test code from your program, and add this program at the end:
# Choose colours and size
color("sky blue", "white")
bgcolor("black")
size = 400
order = 0
# Ensure snowflake is centred
penup()
backward(size/1.732)
left(30)
pendown()
# Make it fast
tracer(100)
hideturtle()
begin_fill()
# Three Koch curves
for i in range(3):
koch(size, order)
right(120)
end_fill()
# Make the last parts appear
update()
Save and run. This should give you a big, white triangle.
Adjust size so it nicely fills the drawing window when run.
Now set order to 6 or 7.
Run the program and enjoy the result.
How many sides does this have? (Hint: every time the order goes up by one, there are 4 times as many.)